Python Basics with Numpy

(from CS230-Deep-Learning)

이 과제 후 당신은 다음을 할 수 있게 됩니다.

• iPython 노트북을 사용할 수 있습니다.
• numpy 함수와 numpy 행렬/벡터 연산을 사용할 수 있습니다.
• "broadcast"의 개념 이해
• 코드의 벡터화 가능

iPython Notebooks

iPython 노트북은 웹 페이지에 포함 된 대화 형 코딩 환경입니다. 이 수업에서는 iPython 노트북을 사용하게 됩니다. ### START CODE HERE ### 및 ### END CODE HERE ### 주석 사이에 코드를 작성하기만하면 됩니다. 코드를 작성한 후 "SHIFT"+"ENTER"를 누르거나 노트북 상단 표시 줄에 있는 "Run Cell"(재생 기호로 표시)을 클릭하여 셀을 실행할 수 있습니다.

(1) 연습 : 아래 셀에서 test를 "Hello World"로 설정하여 "Hello World"를 인쇄하고 아래 셀을 실행합니다.

### START CODE HERE ### (≈ 1 line of code)

### END CODE HERE ###
print ("test: " + test)

test: Hello World

Expected output: test: Hello World

• Shift + Enter (또는 "Run Cell")를 사용하여 셀 실행
• Python 3 만 사용하여 지정된 영역에 코드 작성
• 지정된 영역(### .. 이 영역 .. ###) 밖에서 코드를 수정하지 마십시오.

1. numpy로 기본 함수 만들기 ¶

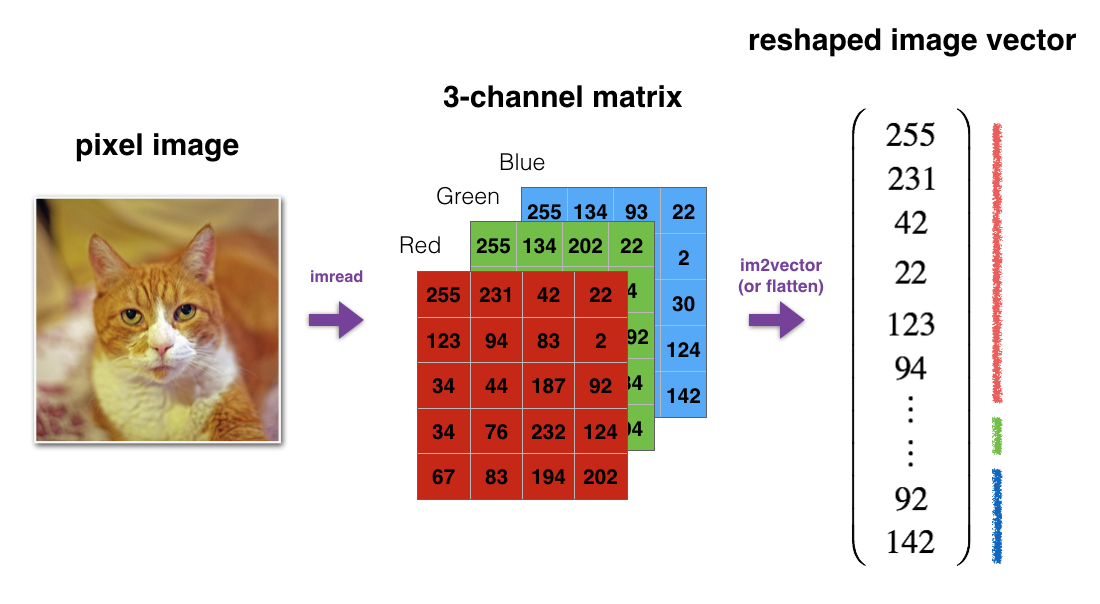
Numpy는 Python의 과학 컴퓨팅을 위한 기본 패키지입니다. 대규모 커뮤니티 (www.numpy.org)에서 관리합니다. 이 연습에서는 np.exp, np.log 및 np.reshape 와 같은 몇 가지 주요 numpy 함수를 학습합니다. 향후 과제을 위해 이러한 함수를 사용하는 방법을 알아야 합니다.

1.1 시그모이드 함수, np.exp( )

np.exp( )를 사용하기 전에 math.exp( )를 사용하여 시그모이드 함수를 구현합니다. 그러면 np.exp( )가 math.exp( )보다 더 나은 이유를 알 수 있습니다.

(2) 연습 : 실수 $x$의 시그모이드를 반환하는 함수를 만듭니다. 지수 함수에는 math.exp(x)를 사용하십시오.

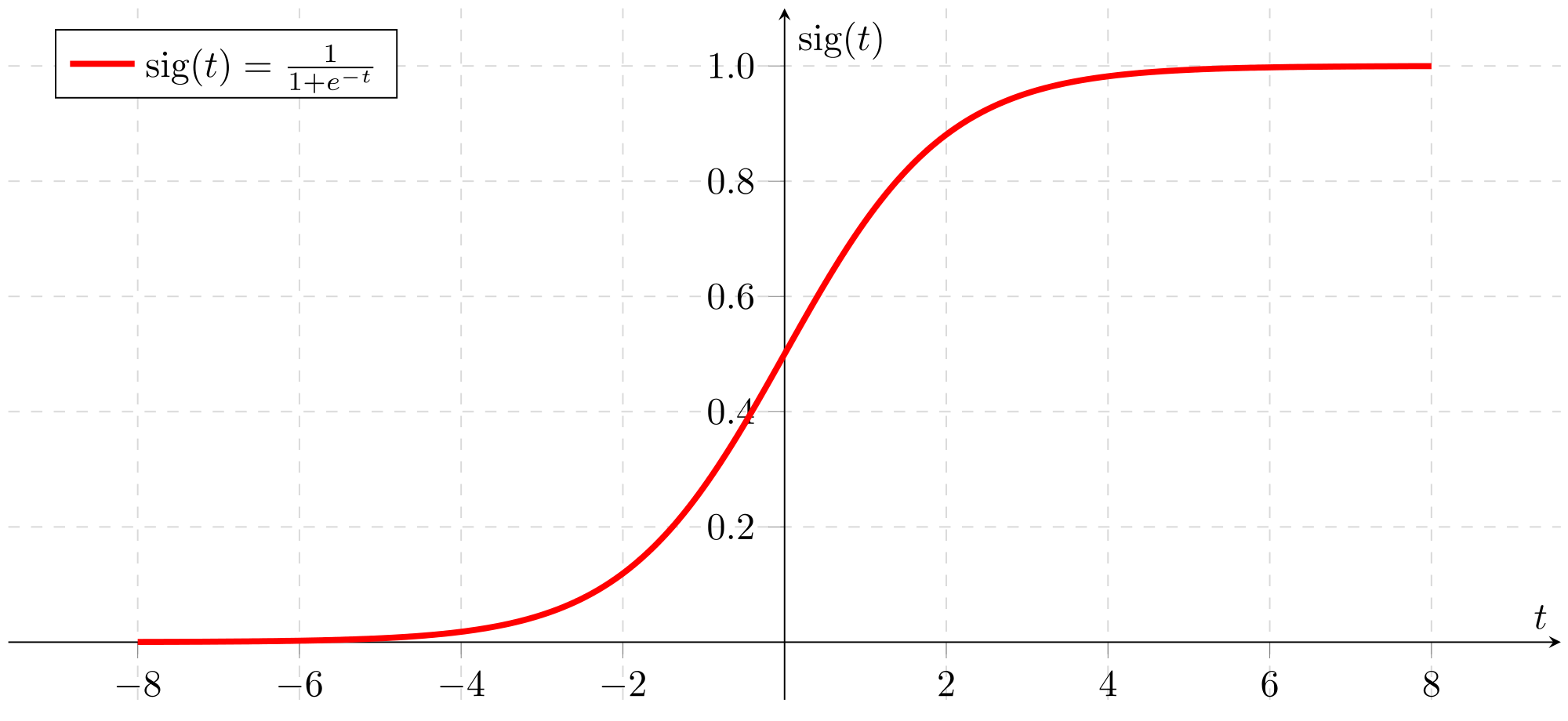
참고 : $sigmoid(x) = \frac{1}{1 + e^{-x}} $는 때때로 로지스틱 함수라고도 합니다. 머신러닝(로지스틱 회귀)뿐 아니라 딥 러닝에서도 사용되는 비선형 함수입니다.

특정 패키지에 속하는 함수를 참조하려면 package_name.function( )을 사용하여 호출할 수 있습니다. 아래 코드를 실행하여 math.exp( )를 사용한 예제를 확인하십시오.

import math

def basic_sigmoid(x):
    """
    Compute sigmoid of x
    Arguments: x -- A scalar
    Return: s -- sigmoid(x)
    """
    ### START CODE HERE ### (≈ 1 line of code)

    ### END CODE HERE ###
    
    return s

basic_sigmoid(3)

0.9525741268224334

Expected output:

basic_sigmoid(3)

0.9525741268224334

"math" 라이브러리는 함수의 입력이 실수이기 때문에 실제로 딥 러닝에서 거의 사용하지 않습니다. 딥 러닝에서 우리는 주로 행렬과 벡터를 입력으로 사용합니다. 이것이 numpy가 더 유용한 이유입니다.

### 딥러닝에서 'math'대신에 'numpy'를 사용하는 이유
x = [1, 2, 3]
basic_sigmoid(x) # x가 벡터이기 때문에 실행할 때 오류가 발생하는 것을 볼 수 있습니다.

실제로 $x=(x_1, x_2, ..., x_n)$이 행 벡터이면 np.exp(x)는 x의 모든 요소에 지수 함수를 적용합니다. 따라서 출력은 다음과 같습니다. np.exp(x) $ =(e^{x_1}, e^{x_2}, \cdots, e^{x_n})$

import numpy as np

x = np.array([1,2,3])
print(np.exp(x))

[ 2.71828183  7.3890561  20.08553692]

또한 x가 벡터인 경우 $s = x + 3$ 또는 $s = \frac{1}{x} $와 같은 Python 연산은 s를 x와 동일한 크기의 벡터로 출력합니다.

x = np.array([1,2,3])
print(x+3)

[4 5 6]

(3) 연습 : numpy를 사용하여 sigmoid 함수를 구현합니다.

지시 : $x$는 이제 실수, 벡터 또는 행렬이 될 수 있습니다. 이러한 모양 (벡터, 행렬 ...)을 표현하기 위해 numpy에서 사용하는 데이터 구조를 numpy 배열이라고합니다. 지금은 더 많이 알 필요가 없습니다.

$$\text{ For } x \in \mathbb{R}^n, \quad \text{sigmoid}(x) = \text{sigmoid}\left( \begin{matrix} x_1\\ x_2\\ \vdots \\ x_n \end{matrix}\right) = \left( \begin{matrix} {1 \over 1 + e^{-x_1}} \\ {1 \over 1 + e^{-x_2}}\\ \vdots \\ {1 \over 1 + e^{-x_n}}\end{matrix}\right) $$

import numpy as np

def sigmoid(x):
    ### START CODE HERE ### (≈ 1 line of code)

    ### END CODE HERE ###
    return s

x = np.array([1,2,3])
sigmoid(x)

array([0.73105858, 0.88079708, 0.95257413])

Expected Output:

sigmoid([1,2,3])

array([ 0.73105858, 0.88079708, 0.95257413])

1.2 Sigmoid gradient

강의에서 보았듯이 역전파를 사용하여 손실 함수를 최적화하려면 그래디언트를 계산해야 합니다. 첫 번째 그래디언트 함수를 코딩해 보겠습니다.

(4) 연습 : sigmoid_grad() 함수를 구현하여 입력 x에 대한 시그모이드 함수의 기울기를 계산합니다. 공식은 다음과 같습니다.

$$ \text{sigmoid_derivative}(x) = \sigma'(x) = \sigma(x)(1-\sigma(x)) \tag{2} $$

종종 이 함수를 두 단계로 코딩합니다.

1. s를 x의 시그모이드로 설정합니다. sigmoid(x) 함수가 유용하다는 것을 알 수 있습니다.
2. $ \sigma'(x) = s(1-s)$ 를 계산합니다.

def sigmoid_derivative(x):
    """
    입력 x에 대한 시그모이드 함수의 그래디언트(기울기 또는 미분이라고도 함)를 계산합니다.
    시그모이드 함수의 출력을 변수에 저장한 다음, 이를 사용하여 기울기를 계산할 수 있습니다.
    """
    ### START CODE HERE ### (≈ 2 line of code)

    
    ### END CODE HERE ###
    return ds

x = np.array([1,2,3])
print("sigmoid_derivative(x) = " + str(sigmoid_derivative(x)))

sigmoid_derivative(x) = [0.19661193 0.10499359 0.04517666]

Expected Output:

sigmoid_derivative([1,2,3])

[ 0.19661193 0.10499359 0.04517666]

배열 재구성(reshaping)

딥 러닝에서 자주 사용되는 두 가지 일반적인 numpy 함수는 np.shape() 와 np.reshape()입니다.

• X.shape는 행렬/벡터 X의 모양(차원)을 얻는 데 사용됩니다.
• X.reshape(...)는 X를 다른 차원으로 재구성하는 데 사용됩니다.

예를 들어, 컴퓨터 과학에서 이미지는 $(길이,높이,깊이=3)$ 모양의 3D 배열로 표현됩니다. 그러나 이미지를 알고리즘의 입력으로 읽으면 $(length * height * 3, 1)$ 모양의 벡터로 변환합니다. 즉, 3D 배열을 1D 벡터로 "풀거나" 모양을 변경합니다.

(5) 연습 : 입력 모양 (길이, 높이, 3)을 취하고, (길이*높이*3, 1) 형태의 벡터를 반환하는 image2vector()를 구현합니다. 예를 들어, 모양 (a, b, c)의 배열 v를 모양의 벡터 (a*b,c)로 재구성하려면 다음을 수행하십시오.

v = v.reshape((v.shape[0] * v.shape[1], v.shape[2])) # v.shape[0] = a; v.shape[1] = b; v.shape[2] = c

이미지의 크기를 상수로 하드 코딩하지 마십시오. 대신 image.shape[0] 등으로 필요한 양을 찾으십시오.

def image2vector(image):
    """
    Argument: image -- a numpy array of shape (length,height,depth)
    
    Return : v -- a vector of shape (length*height*depth, 1)
    """
    ### START CODE HERE ### (≈ 1 line of code)

    ### END CODE HERE ###
    return v

image = np.array([[[ 0.67826139,  0.29380381],
        [ 0.90714982,  0.52835647],
        [ 0.4215251 ,  0.45017551]],

       [[ 0.92814219,  0.96677647],
        [ 0.85304703,  0.52351845],
        [ 0.19981397,  0.27417313]],

       [[ 0.60659855,  0.00533165],
        [ 0.10820313,  0.49978937],
        [ 0.34144279,  0.94630077]]])

print("image2vector(image) = ", image2vector(image))

image2vector(image) =  [[0.67826139]
 [0.29380381]
 [0.90714982]
 [0.52835647]
 [0.4215251 ]
 [0.45017551]
 [0.92814219]
 [0.96677647]
 [0.85304703]
 [0.52351845]
 [0.19981397]
 [0.27417313]
 [0.60659855]
 [0.00533165]
 [0.10820313]
 [0.49978937]
 [0.34144279]
 [0.94630077]]

Expected Output:

image2vector(image)

[[ 0.67826139] [ 0.29380381] [ 0.90714982] [ 0.52835647] [ 0.4215251 ] [ 0.45017551] [ 0.92814219] [ 0.96677647] [ 0.85304703] [ 0.52351845] [ 0.19981397] [ 0.27417313] [ 0.60659855] [ 0.00533165] [ 0.10820313] [ 0.49978937] [ 0.34144279] [ 0.94630077]]

1.4 행 정규화

머신러닝 및 딥러닝에서 사용하는 또 다른 일반적인 기술은 데이터를 정규화하는 것입니다. 경사하강법은 정규화 후 더 빨리 수렴하기 때문에 종종 더 나은 성능으로 이어집니다. 여기서 정규화란 x를 $\frac {x}{\| x \|} $ (x의 각 행 벡터를 그것의 크기(norm)로 나눕니다).

예를 들어 $$x = \begin{bmatrix} 0 & 3 & 4 \\ 2 & 6 & 4 \\ \end{bmatrix}\tag{3}$$ 이면, 그 행들의 크기는 $$\| x\| = \text{np.linalg.norm}(x, \text{axis}=1, \text{keepdims}=True) = \begin{bmatrix} 5 \\ \sqrt{56} \\ \end{bmatrix}\tag{4} $$ 가 되고, 따라서 정규화는 다음과 같다. $$ \text{x_normalized} = \frac{x}{\| x\|} = \begin{bmatrix} 0 & \frac{3}{5} & \frac{4}{5} \\ \frac{2}{\sqrt{56}} &\frac{6}{\sqrt{56}}& \frac{4}{\sqrt{56}} \\ \end{bmatrix}\tag{5}$$

다양한 크기의 행렬로 나눌 수 있으며 잘 작동합니다 : 이것을 브로드캐스팅(broadcasting)이라고 하며, 이 과제의 마지막 부분에서 이에 대해 배울 것입니다.

(6) 연습 : normalizeRows()를 구현하여 행렬의 행을 정규화하십시오. 이 함수를 입력 행렬 x에 적용한 후 x의 각 행은 단위 길이(길이가 1인)의 벡터여야 합니다.

def normalizeRows(x):
    """
    Argument: x -- A numpy matrix of shape (n, m)
    Returns: x -- A normalized (by row) numpy matrix
    """
    ### START CODE HERE ### (≈ 2 lines of code)

    
    ### END CODE HERE ###
    return x

x = np.array([[0,3,4],[1,6,4]])
print("normalizeRows(x) = ", normalizeRows(x))

normalizeRows(x) =  [[0.         0.6        0.8       ]
 [0.13736056 0.82416338 0.54944226]]

Expected Output:

normalizeRows(x)

[[ 0. 0.6 0.8 ] [ 0.13736056 0.82416338 0.54944226]]

참고 : normalizeRows( )에서 x_norm 및 x의 모양을 출력한 다음 평가를 다시 실행할 수 있습니다. 모양이 다르다는 것을 알게 될 것입니다. x_norm이 x의 각 행의 norm을 취한다는 점을 감안할 때 이것은 정상입니다. 따라서 x_norm에는 동일한 수의 행이 있지만 열은 1 개뿐입니다. 그렇다면 x를 x_norm으로 나눌 때 어떻게 작동했을까요? 이것을 broadcast 라고 하는데 지금부터 이야기하겠습니다!

1.5 브로드캐스트 및 softmax 함수

numpy에서 이해해야 할 매우 중요한 개념은 "브로드캐스트"입니다. 서로 다른 모양의 배열 간에 수학적 연산을 수행하는 데 매우 유용합니다. 브로드캐스트에 대한 자세한 내용은 공식 브로드캐스트 문서를 참조하세요.

(7) 연습 : numpy를 사용하여 softmax 함수를 구현합니다. 알고리즘이 둘 이상의 클래스를 분류해야 할 때 사용되는 정규화 함수로 소프트 맥스를 생각할 수 있습니다. 이 전문 과정의 두 번째 과정에서 소프트맥스에 대해 자세히 알아 봅니다.

지시 :

• $ \text{for } \mathbf{x} \in \mathbb{R}^{1\times n}, \quad \text{softmax}(\mathbf{x}) = \text{softmax}(\begin{bmatrix} x_1& x_2& \cdots& x_n \end{bmatrix}) = \begin{bmatrix} \frac{e^{x_1}}{\sum_{j}e^{x_j}} & \frac{e^{x_2}}{\sum_{j}e^{x_j}} & \cdots& \frac{e^{x_n}}{\sum_{j}e^{x_j}} \end{bmatrix} $

• $\text{for a matrix } X \in \mathbb{R}^{m \times n}, x_{ij} \text{ maps to the element in the i-th row and j-th column of x, thus we have: }$ $$\text{softmax}(X) = \text{softmax} \begin{bmatrix} x_{11} & x_{12} & x_{13} & \dots & x_{1n} \\ x_{21} & x_{22} & x_{23} & \dots & x_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \ x_{m1} & x_{m2} & x_{m3} & \dots & x_{mn} \end{bmatrix} = \\ \begin{bmatrix} \frac{e^{x_{11}}}{\sum_{j}e^{x_{1j}}} & \frac{e^{x_{12}}}{\sum_{j}e^{x_{1j}}} & \frac{e^{x_{13}}}{\sum_{j}e^{x_{1j}}} & \dots & \frac{e^{x_{1n}}}{\sum_{j}e^{x_{1j}}} \\ \frac{e^{x_{21}}}{\sum_{j}e^{x_{2j}}} & \frac{e^{x_{22}}}{\sum_{j}e^{x_{2j}}} & \frac{e^{x_{23}}}{\sum_{j}e^{x_{2j}}} & \dots & \frac{e^{x_{2n}}}{\sum_{j}e^{x_{2j}}} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \frac{e^{x_{m1}}}{\sum_{j}e^{x_{mj}}} & \frac{e^{x_{m2}}}{\sum_{j}e^{x_{mj}}} & \frac{e^{x_{m3}}}{\sum_{j}e^{x_{mj}}} & \dots & \frac{e^{x_{mn}}}{\sum_{j}e^{x_{mj}}} \end{bmatrix} = \begin{pmatrix} \text{softmax(first row of X)} \\ \text{softmax(second row of X)} \\ ... \\ \text{softmax(last row of X)} \\ \end{pmatrix}$$

참고

"훈련 예제 수"를 나타내는데 "m"이 사용되며, 각 훈련 예제는 행렬의 각 열에 있습니다. 또한 각 특징(feature)은 각 행에 있습니다 (각 행에는 동일한 특징에 대한 데이터가 있음). Softmax 는 각 훈련 예제의 모든 특징들에 대해 수행되어야 하므로 Softmax는 열에 대해 수행됩니다 (이 과정의 뒷부분에서 해당 표현으로 전환하면).

그러나, 이 코딩 연습에서는 Python에 익숙해지는 데 초점을 맞추고 있으므로 일반적인 수학 표기법 $ m \times n $을 사용합니다. 여기서 $ m $는 행 수이고 $ n $는 열 수입니다.

def softmax(x):
    """
    Argument: x -- A numpy matrix of shape (m,n)
    Returns: s -- A numpy matrix equal to the softmax of x, of shapre (m,n)
    """
    ### START CODE HERE ### (≈ 3 lines of code)
    # Apply exp() element-wise to x. Use np.exp(...).
    x_exp = 
    # Create a vector x_sum that sums each row of x_exp. Use np.sum(..., axis = 1, keepdims = True).
    x_sum =   
    # Compute softmax(x) by dividing x_exp by x_sum. It should automatically use numpy broadcasting.
    s = 
    ### END CODE HERE ###
    return s

x = np.array([[9,2,5,0,0],[7,5,0,0,0]])
print("softmax(x) = ", softmax(x))

y = np.array([[9],[5]])
print(y.shape)
print('x / y = ', x / y)

x_exp - shape: (2, 5)
x_sum - shape (2, 1)
softmax(x) =  [[9.80897665e-01 8.94462891e-04 1.79657674e-02 1.21052389e-04
  1.21052389e-04]
 [8.78679856e-01 1.18916387e-01 8.01252314e-04 8.01252314e-04
  8.01252314e-04]]
(2, 1)
x / y =  [[1.         0.22222222 0.55555556 0.         0.        ]
 [1.4        1.         0.         0.         0.        ]]

Expected Output:

softmax(x)

[[ 9.80897665e-01 8.94462891e-04 1.79657674e-02 1.21052389e-04 1.21052389e-04] [ 8.78679856e-01 1.18916387e-01 8.01252314e-04 8.01252314e-04 8.01252314e-04]]

주의 :

위의 x_exp, x_sum 및 s의 모양을 인쇄하고 평가 셀을 다시 실행하면 x_sum의 모양이 (2,1)이고 x_exp 및 s의 모양이 (2,5)임을 알 수 있습니다. x_exp / x_sum은 파이썬 브로드케스트로 인해 작동합니다. 축하합니다! 이제 python numpy에 대해 꽤 잘 이해하고 딥 러닝에서 사용할 몇 가지 유용한 기능을 구현했습니다.

• np.exp(x)는 모든 np.array x에서 작동하며 모든 좌표에 지수 함수를 적용합니다.
• sigmoid 함수와 그 기울기
• image2vector는 일반적으로 딥 러닝에 사용됩니다.
• np.reshape가 널리 사용됩니다. 앞으로 행렬/벡터 차원을 똑바로 유지하면 많은 버그를 제거할 수 있습니다.
• numpy에는 효율적인 내장 함수들이 있습니다.
• 브로드케스트는 매우 유용합니다

2) 벡터화(Vectorization)

딥 러닝에서는 매우 큰 데이터 세트를 다룹니다. 따라서 계산에 최적화되지 않은 함수는 알고리즘에서 큰 병목 현상이 될 수 있으며 실행하는 데 오랜 시간이 걸리는 모델이 생성 될 수 있습니다. 코드가 계산적으로 효율적인지 확인하려면 벡터화를 사용합니다. 예를 들어, dot/outer/element-wise 곱의 다음 구현 간의 차이점을 살펴보십시오.

import time

x1 = np.random.randn(1000)
x2 = np.random.randn(1000)

### CLASSIC DOT PRODUCT OF VECTORS IMPLEMENTATION ###
tic = time.process_time()
dot = 0
for i in range(len(x1)):
    dot+= x1[i]*x2[i]
toc = time.process_time()
print ("dot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")

### CLASSIC OUTER PRODUCT IMPLEMENTATION ###
tic = time.process_time()
outer = np.zeros((len(x1),len(x2))) # we create a len(x1)*len(x2) matrix with only zeros
for i in range(len(x1)):
    for j in range(len(x2)):
        outer[i,j] = x1[i]*x2[j]
toc = time.process_time()
print ("outer ----- Computation time = " + str(1000*(toc - tic)) + "ms")

### CLASSIC ELEMENTWISE IMPLEMENTATION ###
tic = time.process_time()
mul = np.zeros(len(x1))
for i in range(len(x1)):
    mul[i] = x1[i]*x2[i]
toc = time.process_time()
print ("elementwise multiplication ----- Computation time = " + str(1000*(toc - tic)) + "ms")

### CLASSIC GENERAL DOT PRODUCT IMPLEMENTATION ###
W = np.random.rand(3,len(x1)) # Random 3*len(x1) numpy array
tic = time.process_time()
gdot = np.zeros(W.shape[0])
for i in range(W.shape[0]):
    for j in range(len(x1)):
        gdot[i] += W[i,j]*x1[j]
toc = time.process_time()
print ("gdot = " + str(gdot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")

dot = 4.0683152077212155
 ----- Computation time = 2.544000000000324ms
outer ----- Computation time = 2278.9359999999874ms
elementwise multiplication ----- Computation time = 4.147999999986496ms
gdot = [-18.21280633  -0.26525337 -19.06449536]
 ----- Computation time = 11.392000000000735ms

### VECTORIZED DOT PRODUCT OF VECTORS ###
tic = time.process_time()
dot = np.dot(x1,x2)
toc = time.process_time()
print ("dot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")

### VECTORIZED OUTER PRODUCT ###
tic = time.process_time()
outer = np.outer(x1,x2)
toc = time.process_time()
print ("outer ----- Computation time = " + str(1000*(toc - tic)) + "ms")

### VECTORIZED ELEMENTWISE MULTIPLICATION ###
tic = time.process_time()
mul = np.multiply(x1,x2)
toc = time.process_time()
print ("elementwise multiplication  ----- Computation time = " + str(1000*(toc - tic)) + "ms")

### VECTORIZED GENERAL DOT PRODUCT ###
tic = time.process_time()
dot = np.dot(W,x1)
toc = time.process_time()
print ("gdot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")

dot = 4.068315207721232
 ----- Computation time = 0.4339999999842803ms
outer ----- Computation time = 9.061999999971704ms
elementwise multiplication  ----- Computation time = 0.3859999999917818ms
gdot = [-18.21280633  -0.26525337 -19.06449536]
 ----- Computation time = 1.5880000000265682ms

인식된 것처럼, 벡터화된 구현은 훨씬 깨끗하고 효율적입니다. 더 큰 벡터/행렬의 경우 실행 시간의 차이가 더욱 커집니다.

np.dot()는 행렬-행렬 또는 행렬-벡터 곱셈을 수행합니다. 이것은 요소별 곱셈을 수행하는 np.multiply() 및 연산자 (Matlab/Octave의 .와 동일)와 다릅니다.

2.1 L1 및 L2 손실 함수 구현

(8) 연습 : L1 손실의 numpy 벡터화된 버전을 구현합니다. 함수 abs(x) (x의 절대 값)가 유용하다는 것을 알 수 있습니다.

참조:

• 손실은 모델의 성능을 평가하는 데 사용됩니다. 손실이 클수록 예측($ \hat{y} $)과 실제 값($y$)이 더 많이 다릅니다. 딥 러닝에서는 Gradient Descent와 같은 최적화 알고리즘을 사용하여 모델을 훈련시키고 비용을 최소화합니다.
• L1 손실은 다음과 같이 정의됩니다 : $$\begin{align*} L_1(\hat{y}, y) = \sum_{i=0}^m|\hat{y}^{(i)} - y^{(i)}| \end{align*}\tag{6}$$

def L1(yhat, y):
    """
    Arguments:
    yhat -- vector of size m (predicted labels)
    y -- vector of size m (true labels)
    
    Returns:
    loss -- the value of the L1 loss function defined above
    """
    ### START CODE HERE ### (≈ 1 line of code)

    ### END CODE HERE ###
    
    return loss

yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L1 = " + str(L1(yhat,y)))

L1 = 1.1

Expected Output:

L1

1.1

(9) 연습 : L2 손실의 numpy 벡터화된 버전을 구현합니다. L2 손실을 구현하는 방법에는 여러 가지가 있지만 np.dot() 함수가 유용할 수 있습니다. 참고로 $x=[x_1, x_2, ..., x_n]$ 이면 np.dot(x,x)=$ \sum_{j=0}^n x_j^{2} 입니다.

L2 손실은 다음과 같이 정의됩니다: $$\begin{align*} L_2(\hat{y},y) = \sum_{i=0}^m(\hat{y}^{(i)} - y^{(i)})^2 \end{align*}\tag{7}$$

def L2(yhat, y):
    """
    Arguments:
    yhat -- vector of size m (predicted labels)
    y -- vector of size m (true labels)
    
    Returns:
    loss -- the value of the L2 loss function defined above
    """
    
    ### START CODE HERE ### (≈ 1 line of code)
    # Using function np.dot() useful.

    ### END CODE HERE ###
    
    return loss


yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L2 = " + str(L2(yhat,y)))

L2 = 0.43000000000000005

Expected Output:

L2

0.43

이 과제를 완료한 것을 축하합니다. 이 작은 준비 운동이 향후 과제에 도움이 되기를 바랍니다. 더 흥분되고 흥미로울 것입니다!

• 벡터화는 딥 러닝에서 매우 중요합니다. 계산 효율성과 명확성을 제공합니다.
• L1 및 L2 손실을 검토했습니다.
• np.sum, np.dot, np.multiply, np.maximum 등과 같은 많은 numpy 함수에 익숙해졌습니다.